素因数分解の応用問題 素因数分解を利用した典型的な 応用問題 に次のようなものがあります。 問題 252に自然数aをかけたら、ある別の自然数の平方となった。 最も小さい自然数aを求めよ。 この問題は 素因数分解を利用して解く ことができます
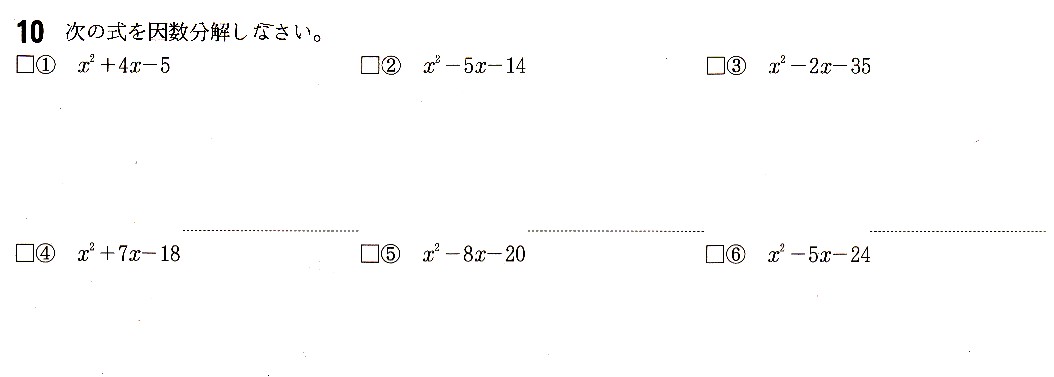
因数分解 中学何年-分解とは、1つにまとまっているものをいくつかのものに分けることです。 ですので、この、因数分解という言葉は簡単にまとめてしまえば、 式を展開 することの逆バージョンであるといえます。 例えば、15という数は、 3×5 で表されます。 この3や5の因数分解 (基本問題1) 因数分解 (基本問題1) 次の式を因数分解しなさい x2 4x 4x2 2x axay x2 3x2 x2 6x5 x2 12x 次の式を因数分解しなさい x2 7x10 x2 11x10 x2 11x30 x2 13x42 x2 6x9 次の式を因数分解しなさい x2 2x35 x2 x30 x2 3x40 x2 18x81 x2 9 x2 16 解説リクエスト
因数分解 中学何年のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
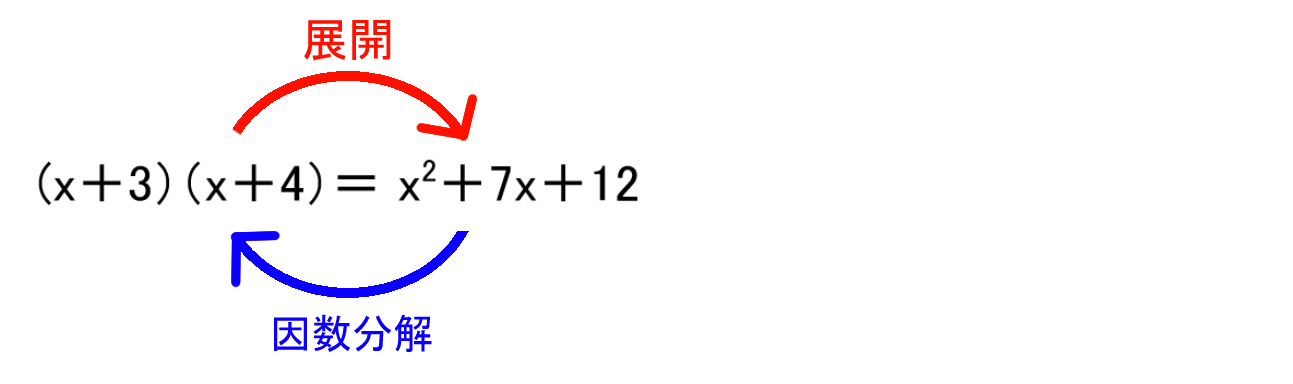 |  | |
 |  | |
 |  |  |
 |  | |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  | |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  |  |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
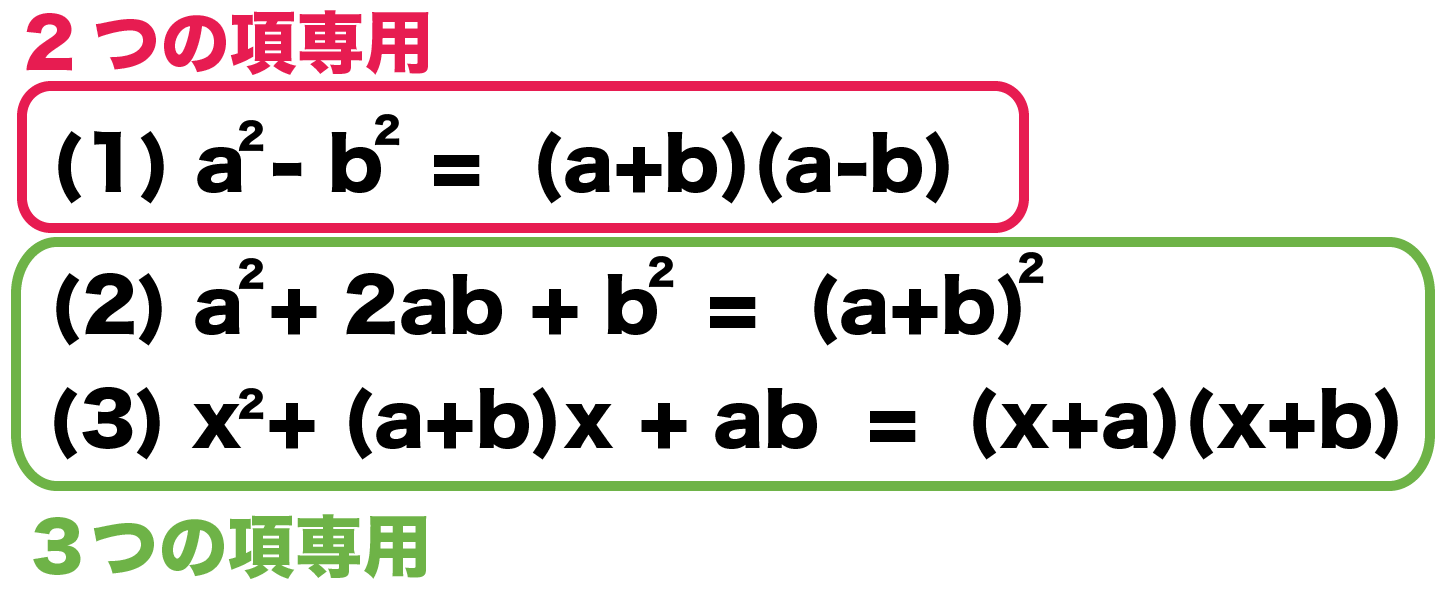 |  |  |
 |  | |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「因数分解 中学何年」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
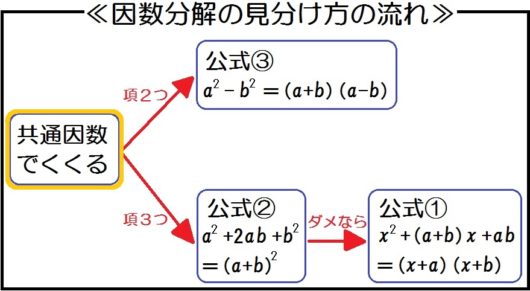
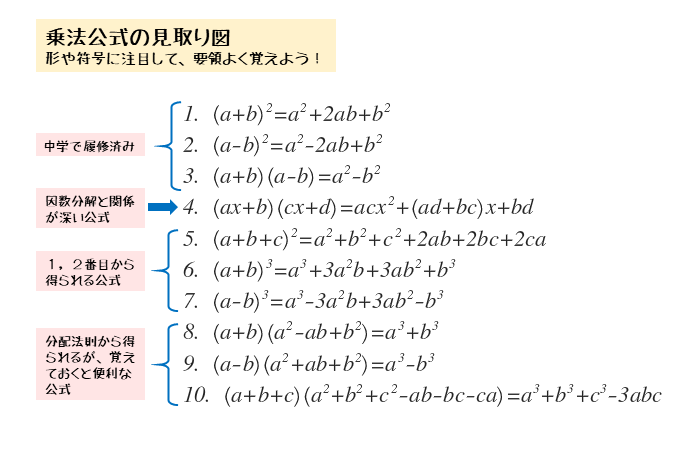
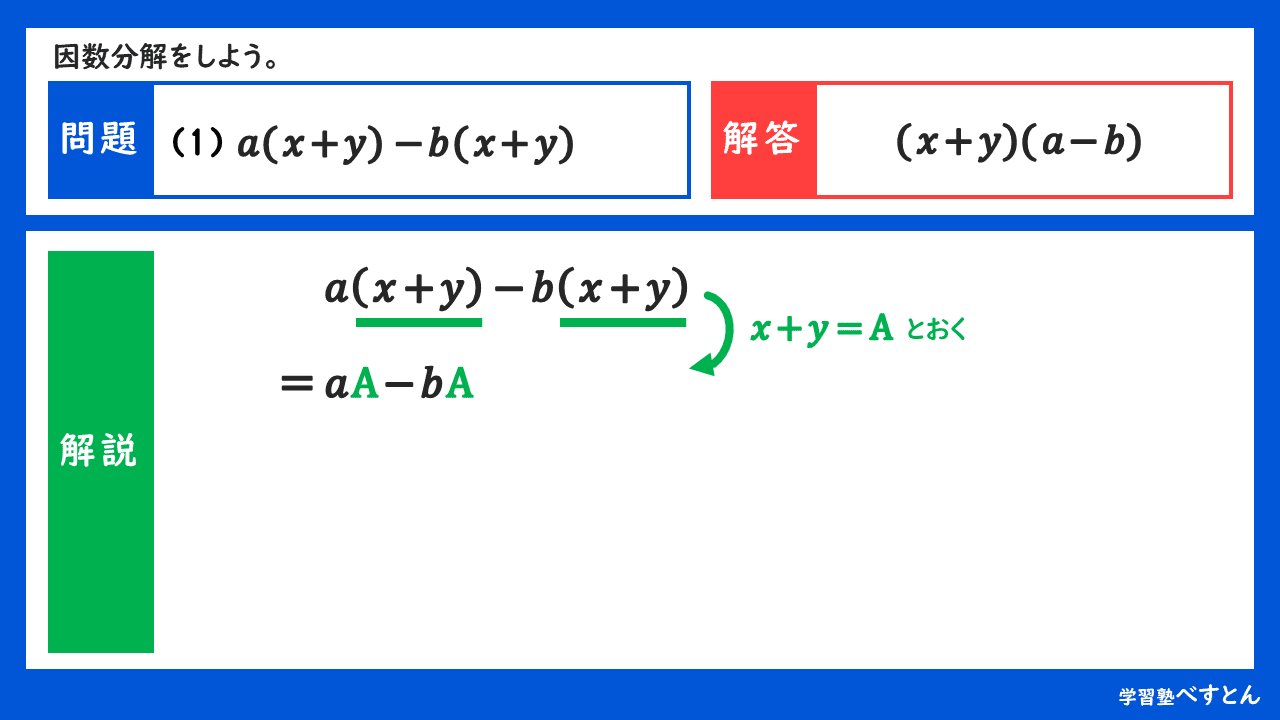
因数分解?? 中学3年生でやる因数分解(いんすうぶんかい) なんだが 言葉を聞くだけで難しそうな問題 ですね笑 でも安心してください! 全然わからないって人でも計算の仕方も解き方のコツさえ知ればカンタンに解ける ようになります。 ではやっていきましょう。関連する学習プリント 中学3年生 数学 計算たしかめミックス 練習問題「式の展開と因数分解」「平方根」「2次方程式」 中学3年生 数学 式の活用 問題プリント 無料ダウンロード・印刷
Incoming Term: 因数分解 中学, 因数分解 中学何年, 因数分解 中学1年生, 因数分解 中学二年生, 因数分解 中学3年, 因数分解 中学 問題, 因数分解中学 難問,




0 件のコメント:
コメントを投稿